clarisson

When one asks a student of Physics what the striking difference between the Quantum and Newtonian theory is, often than not one would claim that Quantum Physics is non-deterministic while Newtonian Physics is the other way around. Such non-determinism is a major hurdle the quantum theory had to overcome, which it managed to do so gracefully. However, it has been known as early as the $70$ ‘s that such non-determinism already manifest itself in Newtonian mechanics. We will illustrate this using what now has come to be known as Norton’s Dome. It is the axially symmetric parametrized surface given as

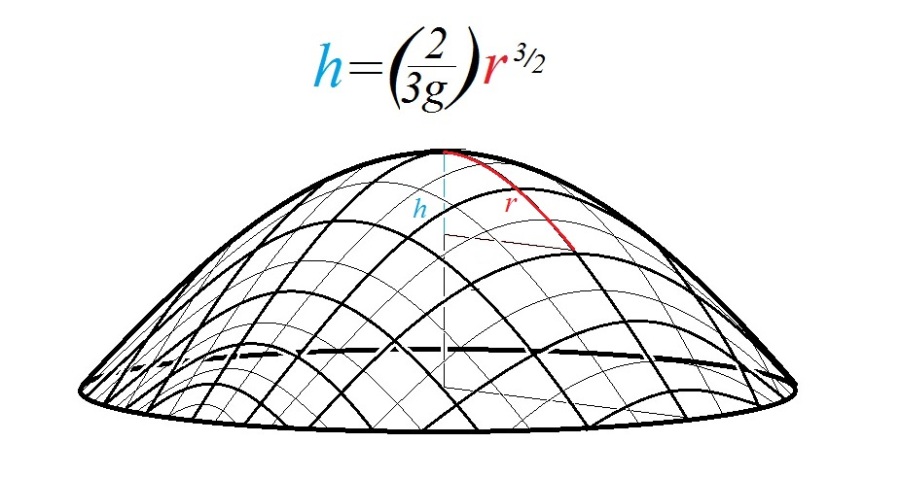
where $g$ denotes the magnitude of the gravitational force, $h$ denotes the vertical distance and $r$ denotes the geodesic distance of a point on the surface from the apex.

Let us talk about what determinism means in the first place. For simplicity, let us consider a particle of unit mass at position $X$ with constant momentum $\stackrel{\rightharpoonup}{p}$ . Then, at any given time $t$ , one can determine the position of the particle, in this case, it is $X+\stackrel{\rightharpoonup}{p}t$ .

Now, consider a ball of unit mass sitting atop Norton’s dome as illustrated below. Take the time to be $t=0$ when the ball is in this position. The question now is, where will the ball be at time $t=1$ ? or any $t>0$ for that matter?

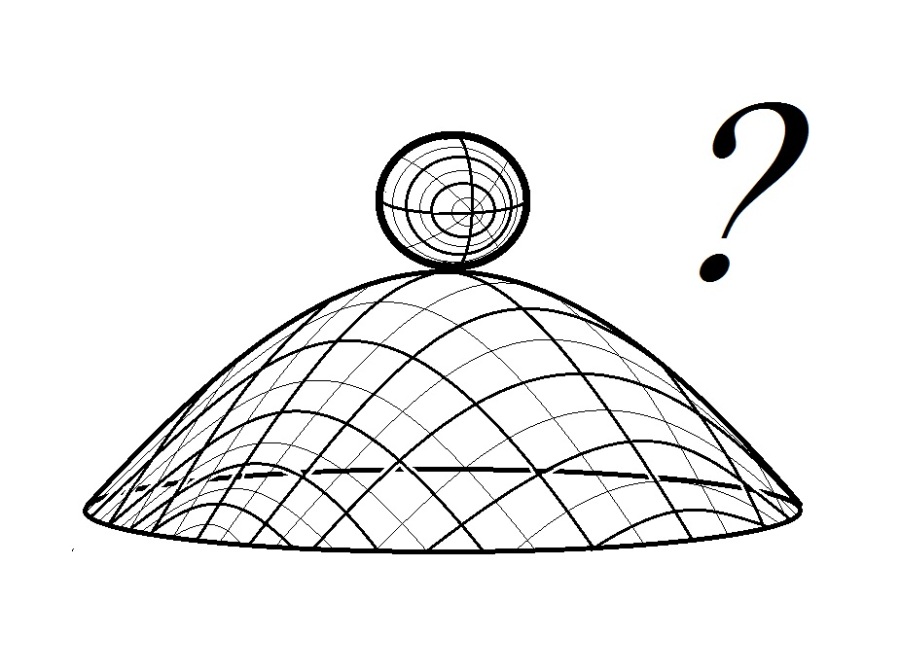
Before we continue, let us mention that such set-up is already forbidden by the uncertainty principle of quantum physics. Note that for the ball to be in this equilibrium state, the center-of-gravity of the ball should be in line with the axis-of-symmetry of the dome. Such set-up determine with full certainty what the position and momentum of the ball is. Let us continue by assuming that such scenario is possible. Let us, for the moment, assume that the ball roll over a particular direction, along a path illustrated as follows.

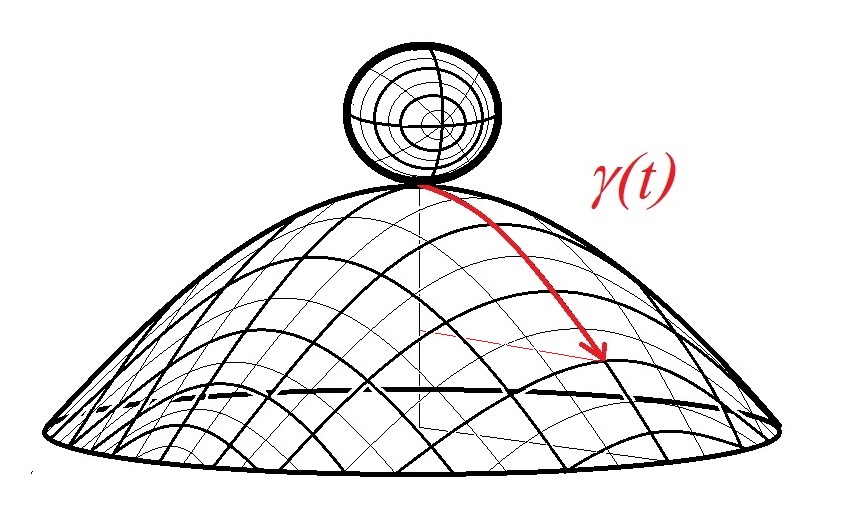
Here, $\gamma(t)$ denotes the geodesic distance of the point of contact of the ball with the dome. The ball is acted upon by gravity.

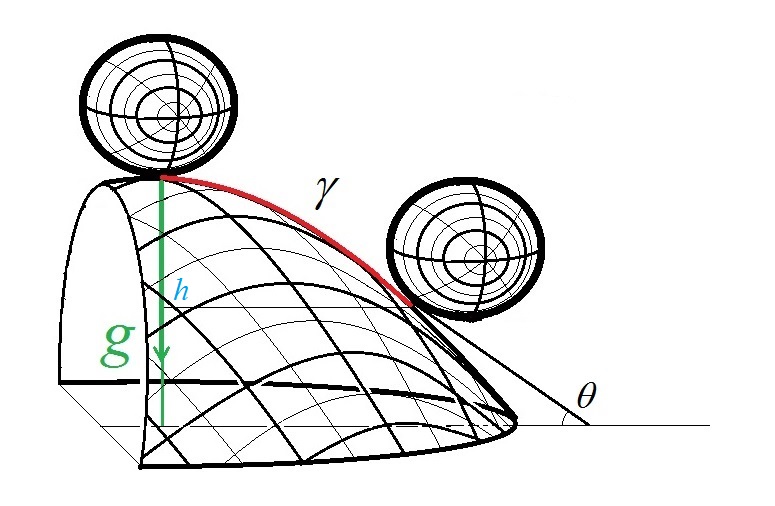
Denoting by $\theta$ the angle made by the tangent line to the point of contact of the ball and the dome with the horizon, we see that the net force $F(t)$ acting on the ball is given by

$F(t)=g\sin \theta(t).$

On the other hand, denoting by $h$ the vertical distance of the point of contact of the ball and the dome from the apex, we have

$\dfrac{dh}{d\gamma}=\sin \theta(t)$

from which follows immediately that

$F(t)=g\dfrac{dh}{d\gamma}.$

By the parametrization of the Norton’s dome, we have

$\dfrac{dh}{d\gamma}=\dfrac{1}{g}\gamma^{1/2}$

from which we get

$F(t)=\gamma(t)^{1/2}.$

By Newton’s second law of motion, $F(t)=ma(t)$ . But we assume the ball has unit mass, thus we have $F(t)=a(t)$ . Since $a(t)=\dfrac{d^{2}\gamma}{dt^{2}}$ , the motion of the ball is governed by the following second-order differential equation

$\dfrac{d^{2}\gamma}{dt^{2}}=\gamma(t)^{1/2}.$

The equation $\gamma(t)=0$ is a solution of the above differential equation. This solution describes the scenario where the ball stays in equilibrium at the top of the dome. However, the above differential equation has other solutions. One such solution is the following

$\gamma(t)= \begin{cases} 0 \ , & 0\leqslant t <\beta \\ & \\ \frac{1}{144}(t-\beta)^{4}, & \beta \leqslant t \end{cases}$

where $\beta>0$ . This solution describes the scenario where the ball stays in equilibrium on top of the dome from $t=0$ to $t=\beta$ and started moving without any additional external force along the path $\gamma$ starting from $t=\beta$ onwards.

Going back to the point we are trying to make, since $\beta$ is arbitrary, it is impossible to predict the future position of the ball given its initial position and momentum. The ball can start rolling whenever it please. Bizarre, right!?

This is an example in which non-determinism exists in the confines of Newtonian mechanics. However, there is a small detail we have to tackle first. The example seems to violate Newton’s First Law of Motion and indeed, during the first version of this post, I originally said so. However, with a discussion with my mathematical physicist friend Daniel Wysocki, we manage to pin down why this isn’t the case. As is known in the physics community, among Newton’s Laws of Motion, the first one is highly non-mathematical in its formulation. When stated as

“(Form 1) An object at rest (or constant velocity) will remain at rest (or constant velocity) unless acted upon by an external force.“

the ball rolling as it please without any additional force seems a contradiction. However, let us adapt the following mathematical formulation of the first law: for an object with momentum $\stackrel{\rightharpoonup}{p}(t)$ and initial position $\stackrel{\rightharpoonup}{X}_{0}$ , we have

(Form 2) $\stackrel{\rightharpoonup}{p} (t) = constant, \ t\in[a,b]$ $\Longrightarrow$ $\stackrel{\rightharpoonup}{X}(t)= \stackrel{\rightharpoonup}{X}_{0} +t\stackrel{\rightharpoonup}{W}, t\in [a,b]$

for some constant vector $\stackrel{\rightharpoonup}{W}$ . Notice that the above interpretation is a consequence of the Second Law. Going back to the second solution $\gamma$ described above, the momentum is zero (and hence, constant) over the time interval $[0,\beta]$ and indeed, the position of the ball is where it should be based on our mathematical interpretation of the First Law. To wrap things up, the ambiguity (or paradox perhaps) is apparent when the First Law is stated in the form (1) rather than in form (2).

Let us close this post by saying that our interpretation of the First Law is by no means unique or universally accepted. It seems that the stance of the physics community about the First Law is not well-defined. One can, for example, consult this site arguing why there is no redundancy in Newton’s Laws of Motion while this paper promotes several interpretation and alternatives to the First Law.

<<previous next>>

Share this: